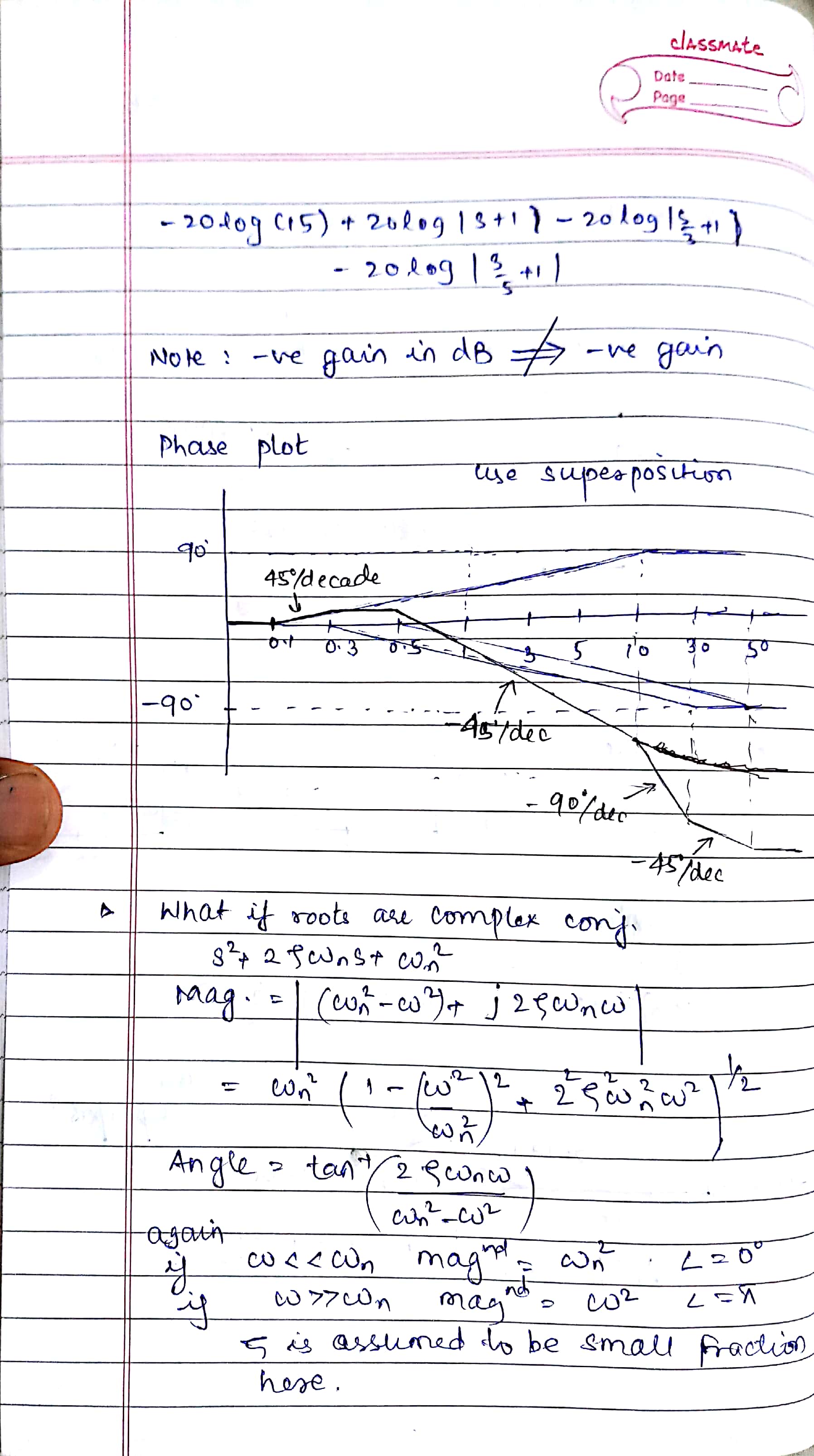
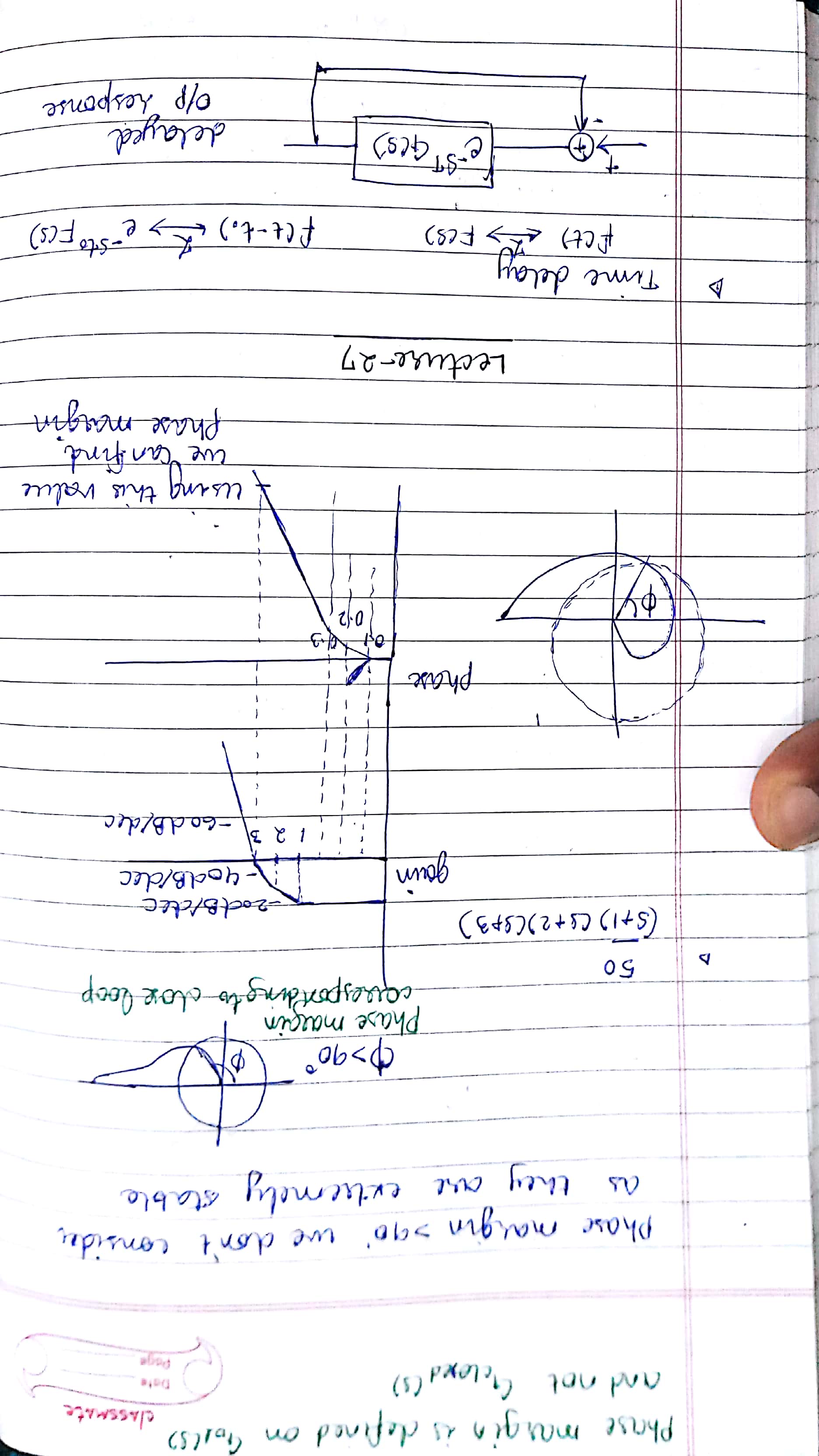
Control Systems
Modeling a system
Series RC circuit
Let \(I(t)\) = output (current), \(v(t)\) = input (applied voltage).
Time-domain equation (series resistor \(R\) and capacitor \(C\)):
\[v(t)=R\,I(t)+\dfrac{1}{C}\displaystyle\int_{t_0}^{t} I(\tau)\,d\tau\]
Assuming zero initial conditions, take Laplace transform (differentiate both sides of the time-domain equation for simplification):
\[V(s)=R\,I(s)+\dfrac{1}{sC}\,I(s)=\Big(R+\dfrac{1}{sC}\Big)I(s)\]
Transfer function from input voltage to current:
\[
\frac{I(s)}{V(s)}=\frac{1}{R+\dfrac{1}{sC}}
=\frac{sC}{sRC+1}.
\]
Two-node/two-branch network
KVL in Laplace transform domain
\[
\begin{pmatrix} V(s) \\ 0 \end{pmatrix}
=
\begin{pmatrix}
R_1+\dfrac{1}{sC_1} & -\dfrac{1}{sC_1} \\[8pt]
-\dfrac{1}{sC_1} & R_2+\dfrac{1}{sC_1}+\dfrac{1}{sC_2}
\end{pmatrix}
\begin{pmatrix} I_1(s) \\ I_2(s) \end{pmatrix}.
\]
Solve using Cramer's rule. Let the coefficient matrix be \(A(s)\) and \(\Delta(s)=\det A(s)\).
\[
\Delta(s)
=\Big(R_1+\frac{1}{sC_1}\Big)\Big(R_2+\frac{1}{sC_1}+\frac{1}{sC_2}\Big)
-\Big(\frac{1}{sC_1}\Big)^2.
\]
Transfer function is given by
\[
I_1(s)=\frac{\det A_1(s)}{\Delta(s)}
\quad\text{and}\quad
I_2(s)=\frac{\det A_2(s)}{\Delta(s)},
\]
Here, \(\det A_1(s)\) is determinant of matrix formed by replacing first column of \(A\) with \(\begin{pmatrix}V(s)\\0\end{pmatrix}\), \(\det A_2(s)\) is determinant of matrix formed by replacing second column of \(A\) with \(\begin{pmatrix}V(s)\\0\end{pmatrix}\).
Mechanical damper system
Damper equation:
\[ F = B\,\frac{dx}{dt} \]
Newton’s law for \(m_2\) gives:
\[
F - k(x_2 - x_1) - B\left(\frac{dx_2}{dt} - \frac{dx_1}{dt}\right)
= m_2\,\frac{d^2x_2}{dt^2}
\]
Newton's law for \(m_1\) gives:
\[
k(x_2 - x_1) + B\left(\frac{dx_2}{dt} - \frac{dx_1}{dt}\right)
= m_1\,\frac{d^2x_1}{dt^2}
\]
The equations can be written in a matrix form:
\[
\begin{pmatrix} F \\ 0 \end{pmatrix}
=
\begin{pmatrix}
k + B\frac{d}{dt} + m_2\frac{d^2}{dt^2} & -k - B\frac{d}{dt} \\[6pt]
-k - B\frac{d}{dt} & k + B\frac{d}{dt} + m_1\frac{d^2}{dt^2}
\end{pmatrix}
\begin{pmatrix} x_2 \\ x_1 \end{pmatrix}
\]
Laplace transform form of the equation is:
\[
\begin{pmatrix} F(s) \\ 0 \end{pmatrix}
=
\begin{pmatrix}
k + sB + s^2 m_2 & -k - sB \\[6pt]
-k - sB & k + sB + s^2 m_1
\end{pmatrix}
\begin{pmatrix} X_2(s) \\ X_1(s) \end{pmatrix}
\]
Using Cramer’s rule, we can find:
\[
\frac{X_2(s)}{F(s)} \quad\text{and}\quad \frac{X_1(s)}{F(s)}.
\]
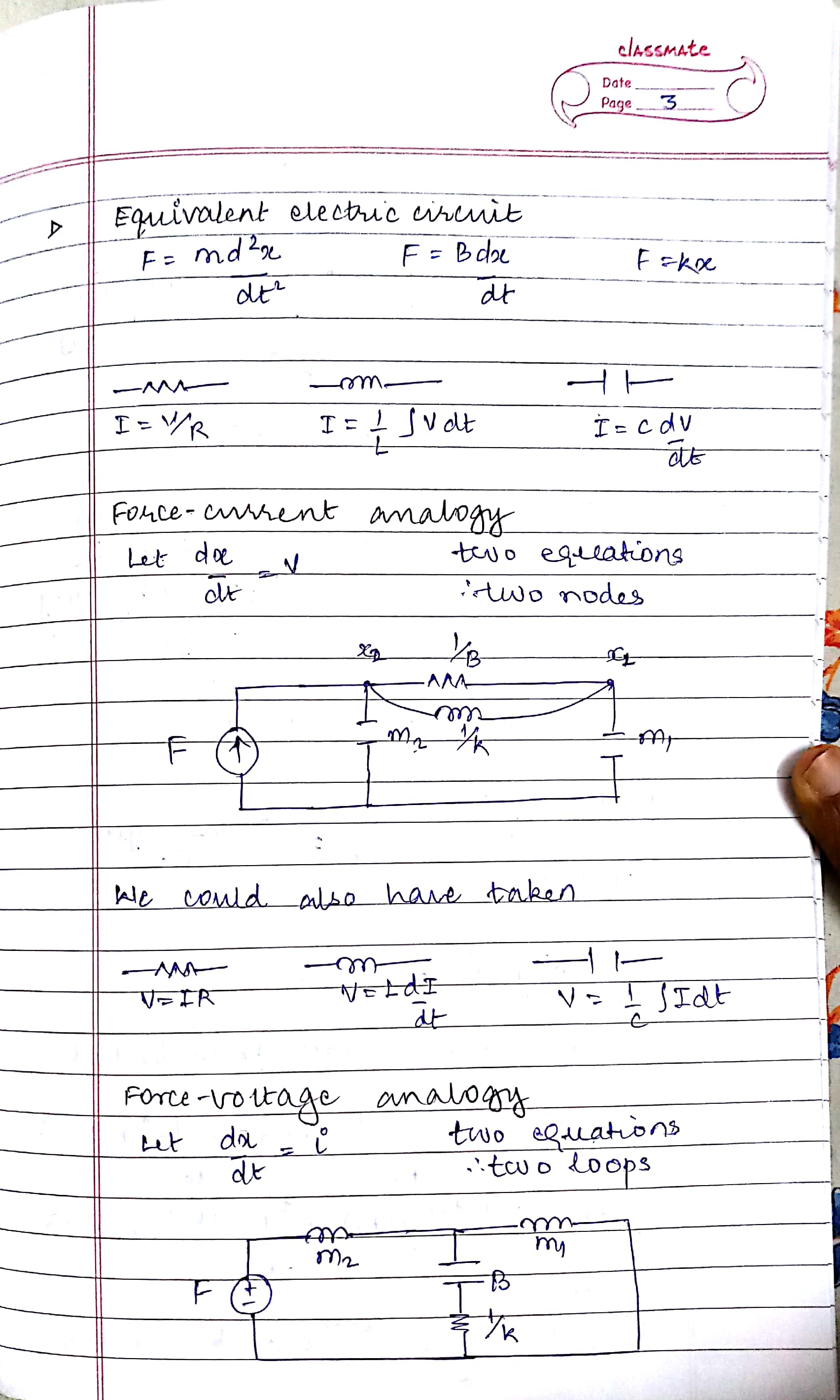
Equivalent electric circuit for mechanical damper system
In the damper system, we have these components:
\[F = m \frac{d^2 x}{dt^2} \quad\quad F = B \frac{dx}{dt} \quad\quad F = kx\]
To convert it into an equivalent electrical circuit, we use the following relations for electrical component
Force–current analogy
Resistor
\[ I = \frac{V}{R} \]
Inductor
\[ I = \frac{1}{L} \int V \, dt \]
Capacitor
\[ I = C \frac{dV}{dt}\]
Let \(\frac{dx}{dt} = v\). Two equations \(\Rightarrow\) Two nodes.
Force–voltage analogy
Resistor
\[V = IR\]
Inductor
\[ V = L \frac{dI}{dt} \]
Capacitor
\[ V = \frac{1}{C} \int I \, dt \]
Let \(\frac{dx}{dt} = i\). Two equations \(\Rightarrow\) Two loops.
Scanned notes
These scanned lecture notes are from the course Control Systems at Indian Institute of Technology, Bombay. Use them at your own discretion. If you would like to help digitize these lecture notes, contact the editor.control system_1.jpg
control system_2.jpg
control system_3.jpg
control system_4.jpg
control system_5.jpg
control system_6.jpg
control system_7.jpg
control system_8.jpg
control system_9.jpg
control system_10.jpg
control system_11.jpg
control system_12.jpg
control system_13.jpg
control system_14.jpg
control system_15.jpg
control system_16.jpg
control system_17.jpg
control system_18.jpg
control system_19.jpg
control system_20.jpg
control system_21.jpg
control system_22.jpg
control system_23.jpg
control system_24.jpg
control system_25.jpg
control system_26.jpg
control system_27.jpg
control system_28.jpg
control system_29.jpg
control system_30.jpg
control system_31.jpg
control system_32.jpg
control system_33.jpg
control system_34.jpg
control system_35.jpg
control system_36.jpg
control system_37.jpg
control system_38.jpg
control system_39.jpg
control system_40.jpg
control system_41.jpg
control system_42.jpg
control system_43.jpg
control system_44.jpg
control system_45.jpg
control system_46.jpg
control system_47.jpg
control system_48.jpg
control system_49.jpg
control system_50.jpg
control system_51.jpg
control system_52.jpg
control system_53.jpg
control system_54.jpg
control system_55.jpg
control system_56.jpg
control system_57.jpg
control system_58.jpg
control system_59.jpg
control system_60.jpg
control system_61.jpg
control system_62.jpg
control system_63.jpg
control system_64.jpg
control system_65.jpg
control system_66.jpg
control system_67.jpg
control system_68.jpg
control system_69.jpg
control system_70.jpg
control system_71.jpg
control system_72.jpg
control system_73.jpg
control system_74.jpg
control system_75.jpg
control system_76.jpg
control system_77.jpg
control system_78.jpg
control system_79.jpg
control system_80.jpg
control system_81.jpg
control system_82.jpg
control system_83.jpg
control system_84.jpg
control system_85.jpg
control system_86.jpg
control system_87.jpg
control system_88.jpg
control system_89.jpg
control system_90.jpg
control system_91.jpg
control system_92.jpg
control system_93.jpg
control system_94.jpg
control system_95.jpg
control system_96.jpg
control system_97.jpg
control system_98.jpg
control system_99.jpg
control system_100.jpg
Author
Anurag Gupta is an M.S. graduate in Electrical and Computer Engineering from Cornell University. He also holds an M.Tech degree in Systems and Control Engineering and a B.Tech degree in Electrical Engineering from the Indian Institute of Technology, Bombay.
Comment
Insert Bullet List
Please enter at least one item.
Item:
Item:
Item:
Item:
Item:
Insert Numeric List
Please enter at least one item.
Item:
Item:
Item:
Item:
Item:
Insert Link
Please enter the link of the website
Optionally you can add display text
Insert Email
Please enter the email address
Optionally add any display text
Insert Image
Please enter the link of the image
Insert YouTube Video
Please enter the link of the video
Image Upload
Privacy Policy
This policy contains information about your privacy. By posting, you are declaring that you understand this policy:
- Your name, rating, website address, town, country, state and comment will be publicly displayed if entered.
- Aside from the data entered into these form fields, other stored data about your comment will include:
- Your IP address (not displayed)
- The time/date of your submission (displayed)
- Your email address will not be shared. It is collected for only two reasons:
- Administrative purposes, should a need to contact you arise.
- To inform you of new comments, should you subscribe to receive notifications.
- A cookie may be set on your computer. This is used to remember your inputs. It will expire by itself.
This policy is subject to change at any time and without notice.
Terms and Conditions
These terms and conditions contain rules about posting comments. By submitting a comment, you are declaring that you agree with these rules:
- Although the administrator will attempt to moderate comments, it is impossible for every comment to have been moderated at any given time.
- You acknowledge that all comments express the views and opinions of the original author and not those of the administrator.
- You agree not to post any material which is knowingly false, obscene, hateful, threatening, harassing or invasive of a person's privacy.
- The administrator has the right to edit, move or remove any comment for any reason and without notice.
Failure to comply with these rules may result in being banned from submitting further comments.
These terms and conditions are subject to change at any time and without notice.
{"commentics_url":"\/\/soln.tech\/comments\/","page_id":201,"enabled_country":false,"country_id":0,"enabled_state":false,"state_id":0,"enabled_upload":true,"maximum_upload_amount":3,"maximum_upload_size":5,"maximum_upload_total":5,"captcha":true,"captcha_url":"http:\/\/soln.tech\/comments\/frontend\/index.php?route=main\/form\/captcha&page_id=201","cmtx_wait_for_comment":"cmtx_wait_for_comment","lang_error_file_num":"A maximum of %d files are allowed to be uploaded","lang_error_file_size":"Please upload files no bigger than %.1f MB in size","lang_error_file_total":"The total size of all files must be less than %.1f MB","lang_error_file_type":"Only image file types are allowed to be uploaded","lang_text_loading":"Loading ..","lang_placeholder_country":"Country","lang_placeholder_state":"State","lang_text_country_first":"Please select a country first","lang_button_submit":"Add Comment","lang_button_preview":"Preview","lang_button_remove":"Remove","lang_button_processing":"Please Wait.."}
{"commentics_url":"\/\/soln.tech\/comments\/","language":"english"}
Similar content
Past Comments