Zero Probability Does Not Mean Impossible

Improbable events are not impossible

How to count a set of infinite size?

point_left_half_square — Random point on the left half of a unit square

Suppose you are given a unit square and asked to choose a point inside it uniformly at random. What is the probability that the point lies in the left half of the square? In problems with a finite number of outcomes, we usually count them to calculate probabilities. However, when dealing with infinitely many possibilities, such as points inside a square, counting no longer works. Instead, we rely on calculating the area of a region. In this case, the left half occupies half the area of the unit square, so the probability is \(\frac{1}{2}\).

Measure on an arbitrary set

In modern probability theory, the concept of area in two dimensions and volume in three dimensions is unified under the single idea of measure. A measure extends the notion of counting from finite sets to arbitrary sets.

Zero probability events

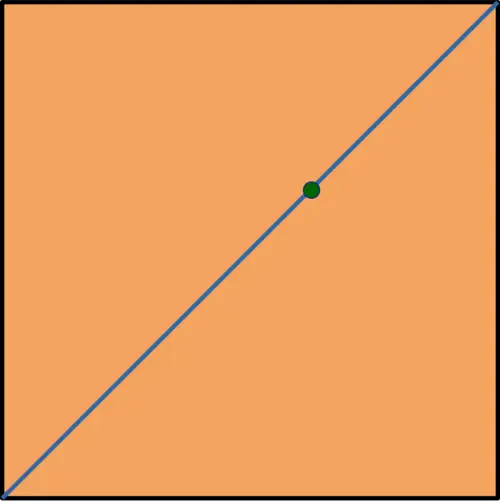
point_diagonal — Random point on the diagonal of a unit square

The measure-theoretic framework helps us handle more subtle questions. For example, consider a modified problem on the unit square. Suppose we draw a line connecting two diagonally opposite corners. What is the probability that a randomly chosen point lies exactly on this line?

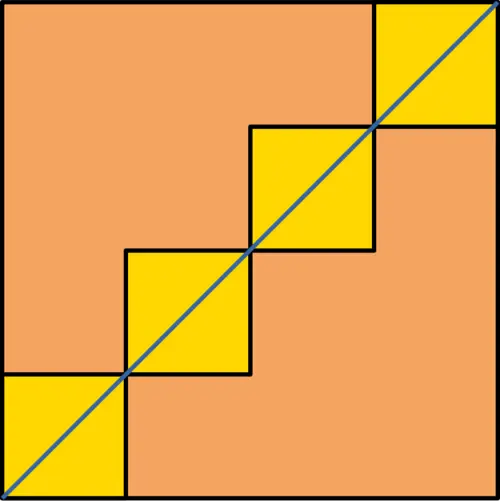
bouding_diagonal — Upper bounding the area of a diagonal with four squares each with sides \(\frac{1}{4}\)

The area of the line is clearly smaller than the area of the unit square. To make this precise, we can cover the diagonal with smaller squares. Start with four squares of side length \(\tfrac{1}{4}\). Together, they give an upper bound on the area of the line as \(\;4 \times \left(\tfrac{1}{4}\right)^2 = \tfrac{1}{4}\).

If we shrink the squares further and use eight squares of side \(\tfrac{1}{8}\), the upper bound becomes \(\;8 \times \left(\tfrac{1}{8}\right)^2 = \tfrac{1}{8}\).

In general, with \(n\) such squares, the upper bound on the area is \(\;n \times \left(\tfrac{1}{n}\right)^2 = \tfrac{1}{n}\).

Since this holds for all \(n\), letting \(n \to \infty\) gives an upper bound of \(0\). On the other hand, by definition, area cannot be negative, so it is at least \(0\). Combining these bounds, we conclude that the area of the line is \(0\).

Therefore, the probability that a randomly chosen point lies exactly on the diagonal is \(0\).

Improbable events are not impossible

If the area of the line is zero, does that mean it doesn’t exist inside the square? Of course not—it clearly exists. This is exactly what we call an improbable event or a zero-probability event. When we say an event is improbable, it does not mean that the event is impossible. Improbable events are those that have zero measure. In theory, improbable events can happen, but in practice, they will not happen almost surely. The key phrase “almost surely” captures the idea that the event has probability zero but is not strictly impossible.

Author

Anurag Gupta is an M.S. graduate in Electrical and Computer Engineering from Cornell University. He also holds an M.Tech degree in Systems and Control Engineering and a B.Tech degree in Electrical Engineering from the Indian Institute of Technology, Bombay.

Comment

Past Comments

No comments yet. Be the first!